理解取模运算(Modulo Operation)
取模运算是数学和计算机科学中常见的一种运算,也称为取余运算。它在很多领域都有广泛的应用,包括编程、密码学、图论等。在计算机编程中,取模运算经常用来解决周期性问题、分组问题以及对数据进行周期性处理的情况。
什么是取模运算?
取模运算是指将两个数相除得到的余数。假设有两个整数a和b,a除以b的余数记作a mod b,读作“a模b”。在数学符号中,通常表示为:
\[a \mod b\]
例如,如果我们计算13除以5的余数,结果为3,因此:
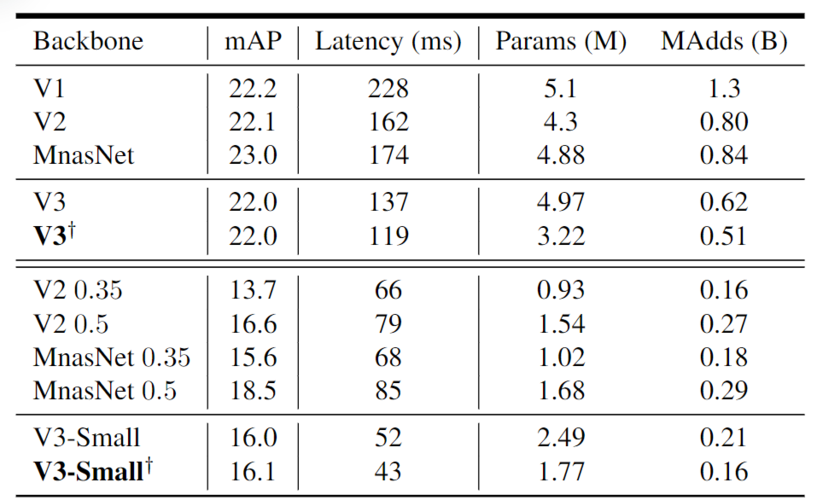
\[13 \mod 5 = 3\]
取模运算的性质
1.
非负性质(NonNegativity)
:取模运算的结果始终为非负数。即使被除数为负数,余数也始终为非负数。2.
循环性质(Cyclic Property)
:当被除数递增或递减时,余数会以循环的方式重复出现。这个性质在处理周期性问题时特别有用。3.
分组性质(Grouping Property)
:取模运算在分组数据时非常有用。例如,我们可以使用取模运算将一组数据分成几个等大小的组。取模运算的应用
1.
周期性处理
:取模运算经常用于处理周期性问题,例如计算星期几、日期处理等。2.
数据分组
:在编程中,可以使用取模运算将一组数据分成固定大小的分组,方便处理。3.
密码学
:取模运算在密码学中有着广泛的应用,例如在加密和解密算法中。4.
图论
:在图论中,取模运算常用于计算图的连通性和路径问题。示例应用
1. 周期性处理
假设我们需要确定某一天是星期几,我们可以使用取模运算:
```python
day_of_week = (day_number starting_day_of_week) % 7
```
其中,`day_number`表示给定日期是一年中的第几天,`starting_day_of_week`表示一年的第一天是星期几。
2. 数据分组
假设我们有一个长度为10的数组,我们想将其分成3组:
```python
array = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
group_size = 3
groups = [[] for _ in range(group_size)]
for i, num in enumerate(array):
group_index = i % group_size
groups[group_index].append(num)
print(groups)
```
输出:
```
[[0, 3, 6, 9], [1, 4, 7], [2, 5, 8]]
```
总结
取模运算是一种重要且常用的运算,在数学和计算机科学中都有广泛的应用。它不仅简单高效,而且能够解决很多实际问题中的周期性和分组性需求。通过灵活运用取模运算,可以更高效地解决各种问题。