高阶导数概念

高阶导数的翻译及其应用

简介：高阶导数是微积分中的重要概念，在数学和工程领域广泛应用。本文将介绍高阶导数的定义、计算方法以及它在不同领域中的应用，以及相关术语的翻译。

1. 高阶导数的定义和计算方法

高阶导数是指对一个函数进行多次求导得到的导数。一阶导数是函数的斜率，而高阶导数则描述了函数斜率的变化率。在数学中通常使用符号表示高阶导数，如f'(x)表示一阶导数，f''(x)表示二阶导数，以此类推。

高阶导数的计算方法可以通过应用一阶导数的定义进行迭代计算。例如，二阶导数可以通过计算一阶导数的导数来得到。对于更高阶的导数，可以采用相同的方法进行计算。还可以使用微分运算符来简化计算，如D^n(f)表示对函数f进行n次求导。

2. 高阶导数的翻译

在中文中，高阶导数通常直接翻译为“高阶导数”。在一些文献或专业场景中，也可以使用“n阶导数”来表示高阶导数。例如，“二阶导数”表示二阶导数。

在其他语言中，翻译的方式可能会有所不同。例如，在英文中，高阶导数通常被称为“higherorder derivatives”。在法语中，可以使用“dérivée d'ordre supérieur”来表示高阶导数。

3. 高阶导数的应用

高阶导数在数学和工程领域有着广泛的应用。

在数学中，高阶导数可以帮助我们更好地理解函数的性质和行为。通过分析高阶导数的正负性、极值点和拐点等特征，可以揭示函数的凸凹性、变化趋势和曲率等信息。这对于优化问题、方程求解和曲线拟合等具有重要意义。

在物理学中，高阶导数可以描述物体在运动中的加速度、速度和位移等变化。例如，在力学中，通过对位移函数进行高阶导数运算可以得到速度和加速度的表达式，从而帮助我们理解物体的运动规律。

在工程领域中，高阶导数可以用于信号处理、图像处理和控制系统设计等应用。例如，在信号处理中，高阶导数可以帮助我们提取信号的特征、辨别信号的类型和进行噪声滤波等操作。在图像处理中，高阶导数可以用于边缘检测、纹理分析和图像分割等任务。

在经济学和金融学中，高阶导数可以应用于市场分析、风险管理和金融衍生品定价等方面。例如，在金融衍生品定价中，通过对期权价格方程进行高阶导数运算可以计算期权的隐含波动率，从而帮助投资者进行风险把握和决策。

结论：

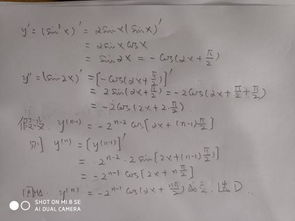
高阶导数是微积分中的重要概念，在数学和工程领域有着广泛的应用。我们可以通过迭代计算一阶导数