最值问题的例题

解决"最值问题" 数学领域

在数学中，“最值问题”是指在一组数据中寻找最大值或最小值的问题。这种问题通常出现在优化理论、经济学、工程学和其他领域。解决最值问题的常见方法包括使用微积分的极值定理、约束条件下的拉格朗日乘数法以及各种优化算法。

寻找函数的最大值和最小值

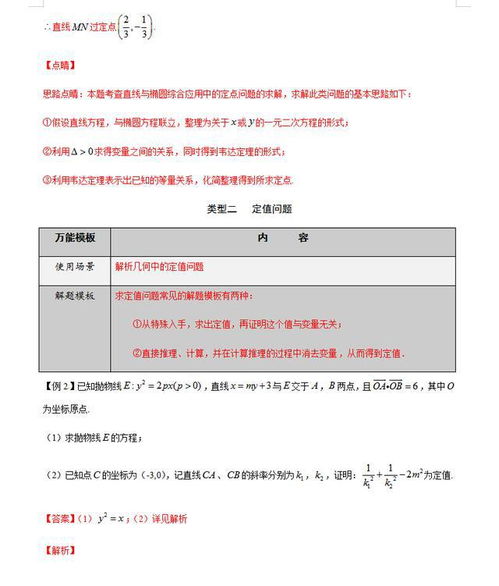
数学中的最值问题通常涉及函数的最大值和最小值。对于一个连续函数，可以通过求解导数为零的点或者使用二阶导数测试来找到其临界点和拐点，从而确定最值所在的区间。

约束条件下的最优化问题

在经济学、工程学和生物学等领域，最值问题通常伴随着一些约束条件。在这种情况下，可以使用拉格朗日乘数法来求解。该方法将约束条件纳入目标函数中，通过构建拉格朗日函数并解其方程，可以找到约束条件下的最值点。

数值优化方法

除了基于微积分的方法外，还可以使用各种数值优化方法来解决复杂的最值问题。这些方法包括梯度下降、遗传算法、模拟退火等，它们在实际问题中得到了广泛的应用。

解决最值问题需要熟练掌握微积分知识以及优化理论，并具备分析问题、建立数学模型和求解的能力。在实际问题中，还需要根据具体情况选择合适的方法并注意结果的合理性和稳定性。