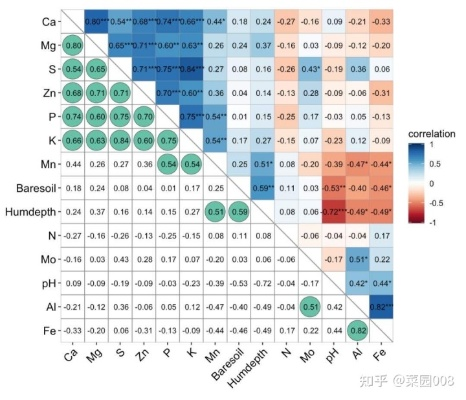
在学术研究和数据科学的广阔领域中,相关系数矩阵无疑是一座重要的桥梁,它将复杂的统计关系以简洁明了的方式呈现出来,作为一名翻译学者,我有幸将这个抽象的数学工具转化为易于理解的语言,以供跨学科团队和非专业人士参考,我们将一起深入剖析这个关键概念,从其定义、计算方法到实际应用中的角色。
相关系数矩阵的定义
相关系数矩阵,又称为皮尔逊相关矩阵或斯皮尔曼等级相关矩阵,是一种衡量变量间线性关系强度和方向的工具,它是一个对称的方阵,其中每一行代表一个变量,每一列对应另一个变量,而矩阵中的每个元素则是两个变量之间的皮尔逊相关系数,其值介于-1(完全负相关)和1(完全正相关),0表示无关联。
计算方法
计算相关系数的过程通常包括以下步骤:
1、计算各变量的均值。
2、计算每个变量对所有其他变量的差分。
3、计算这些差分的协方差。
4、将协方差除以各自的标准差,得到标准化的差分。
5、将标准化差分转换为相关系数。
相关性的类型
相关系数可以分为正相关、负相关和零相关,正相关意味着两个变量在增加时倾向于同步增加,负相关则表示两者在变化上成反比,而零相关表示变量之间没有线性联系。
应用领域
相关系数矩阵在许多领域中发挥着至关重要的作用:
1、社会科学:在经济学、心理学和社会学中,它帮助我们理解个体变量如何相互影响。
2、生物学:在基因表达分析中,它揭示基因间的相互作用。
3、自然科学:物理学中的实验设计常利用相关性来验证假设。
4、市场分析:商业决策中,相关性分析是预测市场趋势的重要工具。
翻译挑战与策略
将专业术语准确地转化为通俗易懂的语言并非易事,我们需要遵循以下原则:
1、简洁明了:避免过于复杂的数学公式,用日常语言解释核心概念。
2、情境化:通过具体的案例,让读者更好地理解相关系数的实际运用。
3、完整性:确保信息全面,包括相关系数的计算方法、不同类型的含义以及应用场景。
通过这样的解读,我们可以跨越语言的障碍,让全球的研究者都能掌握并运用相关系数矩阵这一强大的工具,无论你是数据分析新手还是资深专家,理解并熟练使用相关系数矩阵都将助你更深入地探索世界,发现隐藏的规律。